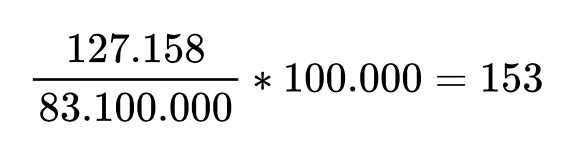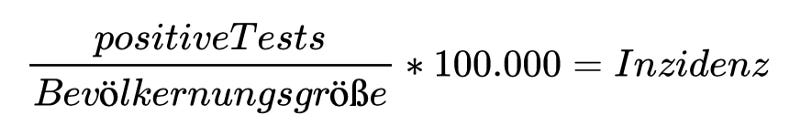Ermächtigung durch Inzidenz
Das private und wirtschaftliche Leben in Deutschland wird zukünftig von der Inzidenz bestimmt, genauer: der COVID-19 Inzidenz. So ist…

Das private und wirtschaftliche Leben in Deutschland wird zukünftig von der Inzidenz bestimmt, genauer: der COVID-19 Inzidenz. So ist deren Verankerung im Dritten Gesetz zum Schutz der Bevölkerung bei einer epidemischen Lage von nationaler Tragweite zu verstehen.
Dort heißt es z.B.
“Bei Überschreitung eines Schwellenwertes von über 50 Neuinfektionen je 100.000 Einwohner innerhalb von sieben Tagen [sind] umfassende Schutzmaßnahmen zu ergreifen, die eine effektive Eindämmung des Infektionsgeschehens erwarten lassen.”, §28a (3)
Als Schutzmaßnahmen werden u.a. gelistet:
“1. Anordnung eines Abstandsgebots im öffentlichen Raum, 2. Verpflichtung zum Tragen einer Mund-Nasen Bedeckung (Maskenpflicht), 3. Ausgangs- oder Kontaktbeschränkungen im privaten sowie im öffentlichen Raum, […]”, §28a (1)
Auf dem Programm steht also das ganze Lockdown Maßnahmenmenü aus 2020/2021. Und die Inzidenz ist der Auslöser für die Maßnahmen bzw. ihre Rücknahme. Darüber muss nicht mehr nachgedacht werden; das Gesetz schreibt vor, dass zu reagieren ist, wenn ein bestimmter Wert erreicht.
Wie genau zu reagieren ist, ist nicht beschrieben; “effektiv” muss es sein. (Dass dem ein Glaube an eine Kausalität zwischen Maßnahmen und Rückgang der Infektionszahlen zugrunde liegt, über den man diskutieren kann, sei hier nicht näher betrachtet.)
Es besteht also noch etwas Spielraum in der Auswahl der Maßnahmen. Dass angeordnet werden muss, ist jedoch zweifelsfrei. Das Bundesgesetz schreibt es für alle Länder einheitlich vor.
Angesichts solcher quasi automatischen Steuerung des öffentlichen und schließlich auch privaten Lebens lohnt sich ein näherer Blick darauf, wie der wöchentliche Wert für diese ermächtigende Inzidenz überhaupt entsteht. Wenn die Regierung das gesellschaftliche Leben ihm anvertraut, sollten alle Bürger auch verstehen woran ihr Leben hängt.
Wie wird die Inzidenz berechnet?
Die Inzidenz ist die Zahl der Neuinfektionen (bzw. der positiven Testergebnisse, z.B. 50) bezogen auf eine normierte Einwohnerzahl (z.B. 100.000).
Die Inzidenz wird berechnet, indem die Zahl der positiven Testergebnisse einer Woche in Bezug zur Bevölkerungsgröße und der normierten Einwohnerzahl gesetzt wird. Das ist ein einfacher Dreisatz:
Beispielrechnung für KW13 2021 auf der Basis von statista Angaben zu durchgeführeten Tests:
Annahme zur Bevölkerungsgröße Einwohner lt. destatis: 83.100.000.
Die Inzidenz ist abhängig von der Prävalenz
Die Inzidenz ist natürlich abhängig davon, wie die Infektionslage ist. Je nach dem wie ein Virus verbreitet ist, steigt oder sinkt die Inzidenz. Darum geht es ja auch beim Gesetz zum Schutz der Bevölkerung: Es soll beobachtet werden, wie sich das Virus ausbreitet. Und wenn es eine gewisse Schwelle überschritten hat, sollen Maßnahmen zur Eindämmung ergriffen werden.
In der KW13 wurden 1.149.279 Tests durchgeführt, die zu den 127.158 positiven Ergebnissen geführt haben. Die Prävalenz (“Durchseuchung”) war in der Woche lt. Tests also 11,06%.
Wäre sie hingegen 12% gewesen, wäre es zu 137.913 positiven Tests gekommen und einer Inzidenz von 166.
Bei einer Prävalenz von 10% andererseits hätte es 114.928 positive Tests gegeben mit einer Inzidenz von 138.
Auf diese Abhängigkeit der Inzidenz von der Prävalenz hebt das Gesetz ab. Die Inzidenz soll die Infektionslage allerdings anschaulicher machen als ein prozentualer Wert. “Inzidenz von 153 pro 100.000” ist für den Normalbürger greifbarer als “Positive Testrate von 11,06%”, hat man sich gedacht. Und warum auch nicht? Oder?
Leider ist es mit der Prävalenz so eine Sache, wie sich weiter unten zeigen wird…
Die Inzidenz ist abhängig von der Anzahl der Tests
Die Inzidenz als griffiger Wert könnte so schön sein, wenn sie denn auch nur von der Infektionslage abhängig wäre. Leider spielen in die Inzidenz aber weitere Faktoren hinein.
Bei gegebener Prävalenz — z.B. 11,06% aus KW13 — ergeben sich die für die Inzidenz von 153 verantwortlichen 127.158 positiven Ergebnisse nur durch Anwendung der Prävalenz auf die Testanzahl:
Genau gesagt ist es ja aber anders herum: Die Prävalenz ist nur eine Annahme aufgrund des Verhältnisses der positiven Tests zur Testanzahl:
Niemand kennt die Prävalenz wirklich. Gerade sie soll ermittelt werden.
Für den Moment sei aber die Prävalenz von 11,06% gesetzt. Was würde dann passieren, wenn mehr oder weniger Tests gemacht worden wären in KW13?
Annahme: 1.411.517 Tests wie in KW12. Dann wäre es zu 156.113 positiven Ergebnissen gekommen, aus denen sich eine Inzidenz von 187 ergeben hätte.
Annahme: 1.060.602 Tests wie in KW06. Die hätten zu 117.302 positiven Tests geführt und damit zu einer Inzidenz von 141.
Bei gegebener Infektionslage ist also die Inzidenz davon abhängig, wieviele Tests gemacht werden. Mehr Tests führen zu mehr positiven Ergebnissen, weil ja die Prävalenz in der getesteten Gruppe ist, wie sie ist. Das Verhältnis von positiven Tests zu Testanzahl ist immer gleich — aber die absolute Zahl positiver Ergebnisse verändert sich mit der Testanzahl. Genau diese absolute Zahl positiver Tests geht ja aber in die Berechnung der Inzidenz ein.
Die Inzidenz ist abhängig von der Bevölkerungsgröße
Ein weiterer Faktor, der die Inzidenz beeinflusst, liegt laut der obigen Formel auch noch auf der Hand: die Bevölkerungsgröße.
Man könnte meinen, die sei nicht entscheidend, weil doch konstant. Doch das stimmt nicht. Menschen sterben, Menschen werden geboren, Menschen wandern zu und ab. Über das Jahr gesehen mag es da schonmal eine Schwankung von vielleicht 30.000 geben und über mehrere Jahre, auf die das Gesetz angelegt ist mit seinen festgelegten Inzidenzwerten, mag die Schwankung sogar größer sein.
Wie verändert sich also die Inzidenz, wenn die Bevölkerung schrumpft oder wächst? Zur Erinnerung: Die obigen Werte — 127.158 positive Tests bei 83.100.000 Einwohnern — führen zu einer Inzidenz von 153,02.
Annahme: 83.050.000 Einwohner. Mit dieser Bevölkerungsgröße wäre die Inzidenz immer noch 153,11.
Annahme: 83.200.000 Einwohner. Bei dieser Bevölkerungsgröße liegt die Inzidenz knapp unter 152,83.
Die Bevölkerungsgröße hat einen Effekt, der ist allerdings nicht sehr ausgeprägt. Pro 100.000 Einwohner verändert sich bei gegebenen positiven Tests die Inzidenz um ca. 0,2.
Die Inzidenz ist von der Güte der Tests abhängig
Die offensichtlichen und deutlichen Abhängigkeiten der Inzidenz sind die von Prävalenz und Testanzahl. Leider ist die Infektionsrate — z.B. 11,06% — aber nicht die reale Prävalenz. Es sind nicht 11,06% aller Menschen infiziert, wenn 11,06% der Tests positiv ausfallen. Ein ganz offensichtlicher Grund: die Tests sind nicht perfekt — wie alles Menschengemachte.
Tests finden nicht jeden Infizierten. Ihre Sensitivität ist nicht 100%, sondern vielleicht nur 99%. D.h. von 100 Infizierten werden 99 korrekt erkannt (true positive), aber einer geht den Tests durch die Lappen (false negative).
Auch identifizieren Tests nicht jeden Menschen ohne Infektion korrekt. Ihre Spezifizität ist vielleicht nur 98%. D.h. von 100 nicht Infizierten würden 98% korrekt erkannt (true negative), aber zwei würden dennoch als positiv gemeldet (false positive).
Es ist also zu erwarten, dass die 127.158 positiven Ergebnisse zu wenige sind, weil den Tests manche Infizierten entgangen sind, andererseits sind es aber auch wahrscheinlich zu viele positive Ergebnisse, weil fälschlicherweise Infektionsfreie positiv ausgewiesen wurden.
Wie groß ist der Effekt der Testgüte auf die Inzidenz? Enthalten die 127.158 positiven Tests eine bedeutende Missweisung?
Wie positive Tests entstehen
Um das herauszufinden, zunächst ein genauerer Blick auf die Berechnung der positiven Ergebnisse. Sie entstehen in drei Schritten. Die seien hier der Verständlichkeit halber mit Phantasiezahlen beschrieben.
(1) Es werden 1.000.000 Tests durchgeführt und die Prävalenz ist 10%. Diese Prävalenz ist eigentlich nicht bekannt, aber sie wird für die Erklärung des Rechenwegs benötigt.
Von den getesteten Menschen sind real 100.000 infiziert. Das ist natürlich auch nicht bekannt, aber wird für die Erklärung der Bestimmung der positiven Tests benötigt.
(2) Wenn ein Test eine Sensitivität von 90% und eine Spezifizität von 80% hat, dann erkennt der Test von diesen 100.000 Infizierten 90.000 (true positive) und weist von den 900.000 nicht infizierten trotzdem 20% (100%- Spezifizität%) als positiv aus: 180.000 (false positive).
(3) Die Zahl positiver Tests ist die Summe der true positive und der false positive Ergebnisse, also
Es sieht mit diesen Beispielzahlen also nun so aus, als seien 270.000 Menschen infiziert und die Prävalenz 27%. Das ist ein eklatanter Unterschied zu den realen Zahlen! Die Testgüte hat also einen u.U. deutlichen Einfluss auf die Zahl der positiven Tests und damit auf die Inzidenz.
Rückrechnung der Prävalenz aus der Zahl positiver Tests
Es ist unschön, keine Idee davon zu haben, was denn die Prävalenz ist. Aber zum Glück kann man die drei Schritte der vorherigen Rechnung auch in umgekehrter Richtung durchlaufen. Ausführlich ist das in diesem Artikel beschrieben: Wo ist die Prävalenz hin?
Die Prävalenz ist also nicht durch Messung bekannt, kann jedoch berechnet werden aus der Testanzahl, den positiven Tests und auf der Basis von Annahmen für die Testgüte.
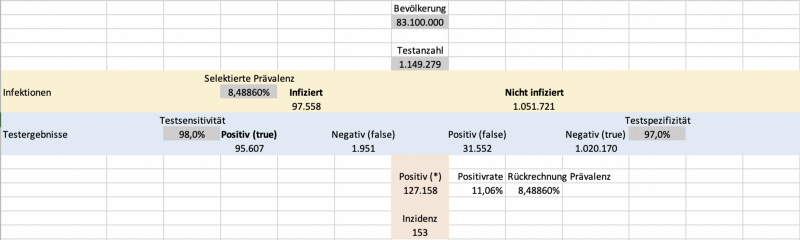
Gegeben sollen wieder 127.158 positive Tests auf 1.149.279 Tests sein. Und die Annahme für die Sensitivität ist 98%, die für die Spezifizität ist 97%. Diese Annahmen sind nicht aus der Luft gegriffen, aber letztlich kommt es nicht auf die exakte Güte an, um eine Idee davon zu bekommen, wie ihr Effekt auf die Inzidenz ist.
Mit diesen Werten führt eine Rückrechnung zu einer Prävalenz von 8,4886%. Durch die (angenommene) mangelnde Testgüte enthält die Zahl von positiven Tests also eine Missweisung von 29.601 vermeintlichen Infektionen. Gemessen wurden 127.158, real existieren jedoch nur 97.558.
Geschuldet ist diese Missweisung vor allem einer mangelnden Spezifizität von 97%. Durch sie entstehen 31.552 falsch positive Ergebnisse. Das ist kein unerheblicher Prozentsatz bei real nur 97.558 infizierten Menschen.
Die Inzidenz aufgrund imperfekter Tests ist 153; die Inzidenz auf Basis der realen Infektionen wäre dagegen nur 117 oder knapp 25% niedriger.
Einfluss der Testgüte auf die Inzidenz
Ob die Testgüte tatsächlich 98%/97% für Sensitivität bzw. Spezifizität ist, ist wohl nicht eindeutig zu bestimmen. Auch Qualitätsprüfungen haben eine Fehlermarge. Vielleicht ist die Güte 98,1%/96,9% oder 97,9%/98,7%?
Bei unbekannter Testgüte ist ihr absoluter Wert daher zunächst uninteressant für die Frage der Auswirkung auf die Inzidenz, den Unterschiede in der Testgüte machen.
Dazu zwei Beispielrechnungen: Vergleichswerte liefer die Zahlen der KW13 mit den Annahmen 98%/97%. Was, wenn sich die Sensitivität um 1% ändert? Was, wenn sich die Spezifizität um 1% ändert?
Annahme: 97%/97%. Mit einem Prozent weniger Sensitivität ist die Inzidenz 152 statt 153 (mit einem Prozent mehr 154).
Annahme: 98%/96%. Mit einem Prozent weniger Spezifizität ist die Inzidenz 166 statt 153 (mit einem Prozent mehr 140).
Der Einfluss der Testgüte liegt also vor allem auf der Spezifizität. Ein Prozent mehr oder weniger macht hier einen deutlich größeren Unterschied als bei der Sensitivität.
Die Inzidenz ist von der selektierten Prävalenz abhängig
Und zum Schluss noch eine subtile Abhängigkeit: Die Inzidenz ist auch noch von der Teststrategie abhängig.
Teil der Teststrategie ist die Zahl der durchgeführten Tests. Wie gezeigt, ist davon die Inzidenz abhängig. Allerdings ist sie noch mehr abhängig von der Prävalenz.
Bei genauerer Betrachtung ist jedoch diese sehr ausschlaggebende Prävalenz nicht “gottgegeben”. Sie ist vielmehr eine “einstellbare Größe”, selbst wenn sie unbekannt ist. Denn sie hängt von einem zweiten Aspekt der Teststrategie ab, dem Selektionskriterium.
Wie zurückgerechnet mag die Prävalenz in der KW13 8,4886% betragen haben. Doch das war nur die Prävalenz in der Gruppe von Menschen, die getestet wurden. Sie sei deshalb genauer die selektierte Prävalenz genannt.
Solange nicht repräsentativ getestet wird, entspricht die selektierte Prävalenz allerdings kaum der realen Prävalenz der ganzen Bevölkerung. Die reale Prävalenz kann höher oder niedriger liegen.
Zwei extreme Beispiele: Wenn nur Neugeborene getestet würden, wäre die selektierte Prävalenz sicherlich eine ganz andere als wenn nur Patienten auf einer Intensivstation getestet würden.
Die Zahl der positiven Tests ist deshalb auch eine Funktion des Selektionskriteriums der Testpersonen: Wer wird überhaupt getestet? Wie ist die Altersverteilung, wie ist die Verteilung der Lebensumstände? Werden dieselben Personen mehrfach getestet? Es gibt viele Fragen, die gestellt werden könnten und deren Antwort bedeuten könnte, dass die selektierte Prävalenz weit von der realen entfernt ist. Die selektierte Prävalenz könnte für die meisten Menschen irrelevant sein.
Vor allem jedoch: Solange nicht streng kontrolliert Woche für Woche dieselben Selektionskriterien angelegt werden, solange ändert sich die selektierte Prävalenz ständig, selbst wenn die reale Prävalenz unverändert ist.
Sensitivitätsanalyse
Die Inzidenz wird also von verschiedenen Größen beeinflusst. Es ist darauf zu achten, dass deren Werte sauber erhoben werden. Doch egal, wie man sich bemüht, es werden Fehler geschehen. Oder es gibt Voreingenommenheiten, die Werte selektieren, wenn es eine Auswahl gibt. Die Frage ist deshalb, wie stark die Inzidenz auf Ungenauigkeiten reagiert. Welchen Ausschlag machen Abweichungen der in die Berechnung eingesetzten Zahlen von den realen?
Ausgangspunkt für eine solche Analyse ist eine Excel-Tabelle mit den bisher benutzen Formeln und den bisher benutzen Zahlen:
Wenn dort Werte für Bevölkerungsgröße, Testanzahl, selektierte Prävalenz, Sensitivität und Spezifizität in verschiedenen Größen eingetragen werden, ergibt sich ein Spektrum von Inzidenzwerten.
Drei verschiedene Werte sollen jeweils zunächst genügen für die Parameter:
Wenn die Berechnung auf die mittleren Werte eingestellt wird, ergibt sich eine Inzidenz von 91. Wie stark die nun von den Parameterwerten abhängt, zeigt sich, wenn jeweils ein Wert variiert wird. Das Ergebnis sieht als Butterfly Chart so aus:
Den größten Unterschied macht die selektierte Prävalenz. Auf sie folgen die Anzahl der Tests und die Spezifizität. Allerdings muss sich die Anzahl der Tests um 40% ändern für eine ähnlich große Veränderung, wie sie eine Veränderung der Spezifizität um nur 2,5% bewirkt.
Ähnlich sieht das Bild auch aus, wenn ein Simulationswerkzeug wie guesstimate die Arbeit übernimmt. Das gezeigte Modell https://www.getguesstimate.com/models/18103…
…weist ebenfalls die selektierte Prävalenz als entscheidenden Einflussfaktor aus:
Unter Berücksichtigungen aller Variationsbreiten und gewissen Annahmen für ihre Wahrscheinlichkeit ergibt sich als Wahrscheinlichkeitsverteilung für die Inzidenz dann dieses Bild:
Solange die selektierte Prävalenz nicht unter 1% sinkt, ist nicht zu erwarten, dass es eine Inzidenz kleiner als 34 geben wird — und selbst das ja nur, wenn alle anderen Parameter günstig stehen (im Rahmen des Modells). Am wahrscheinlichsten ist sogar eine Inzidenz von um die 75.
Ausblick
Die Inzidenz ist zukünftig lebensbestimmend für die Gesellschaft in Deutschland. Die Menschen sind dem Schutz durch das Infektionsschutzgesetz und dem Bevölkerungsschutzgesetz überantwortet — fast könnte man sagen ausgeliefert.
Dieser Schutz würde nun ja aber zu spät greifen, wenn die Inzidenz nicht ständig beobachtet würde. Um die Inzidenz Maßnahmen triggern lassen zu können, muss also ständig getestet werden. Daran ändert auch eine Impfung nichts. Die Impfung führt höchstens dazu, dass die Inzidenz unterhalb der gesetzlichen Triggerwerte bleibt. Ermittelnt werden muss die Inzidenz dennoch.
Es stellt sich also die Frage, wann wieviele getestet wird. Immerhin hat die Testanzahl einen Einfluss auf die Inzidenz — und ist sehr leicht zu kontrollieren. Wird man Ressourcen sparen wollen und vielleicht die Testungen auf 20% herunterfahren, z.B. 250.000 pro Woche? Dann ergäbe sich bei einer Ausgangssituation wie in KW13 eine Inzidenz von 33 statt 153.
Das wäre begrüßenswert — ließe sich jedoch auch aus dem Stand jederzeit ändern. Die Lobby der Testanbieter und Labore könnte dafür plädieren, mehr zu testen: “Sicher ist sicher!”
Es könnte auch Forderungen geben, jahreszeitlich unterschiedlich zu testen. Sollte man nicht im Sommer sparen, wenn die Menschen ohnehin weniger krank sind, dafür aber im Winter mehr testen?
Das hört sich irgendwie plausibel an — führt aber geradewegs in den Lockdown: Das Verfahren führt ja umso eher zu hoher Inzidenz, je mehr getestet wird. Eine steigende Testzahl bei sogar gleichbleibender Prävalenz führt zu einer höheren Inzidenz. Es besteht also die Gefahr, dass man sich in maßnahmenrelevante Inzidenzen hineintestet.
Wenn sich nun die reale Prävalenz über das Jahr ganz natürlich und moduliert durch Maßnahmen entwickelt und auch noch eine künstliche Testanzahl sich verändert, dann besteht die Gefahr von “Stroboskopmaßnahmen”: Es kommt zu einem Flackern von an/aus im ein- oder zweiwöchigen Takt. Ein planbares privates und wirtschaftliches Leben wird dann sehr schwierig.
Je größer die Ausschläge der Maßnahmen, je unvorhergesehener und uneinheitlicher sie über Deutschland verteilt sind, desto weniger verlässlich ist Deutschland in der Folge als Plattform für das Wirtschaften. Es besteht die Gefahr, dass sich Deutschland auf das Niveau eines 3. Welt Landes testet, in das Unternehmen nicht mehr investieren wollen, weil ja nicht gewiss ist, wie lange wie viel gearbeitet werden kann.
Unterm Strich gibt es also zwei Risiken, die sich aus der Verankerung der Inzidenz als Trigger im Gesetz ergeben:
Testanzahl und Testgruppenselektionskriterien können “im besten Willen” so eingesetzt werden, dass sich eine Schwingung im komplexen System der Gesellschaft durch an- und ausgeschaltete Maßnahmen ergibt, die das System nachhaltig schädigen.
Testanzahl und Testgruppenselektionskriterien können zu politischen Zwecken missbraucht werden. Solange nicht klar ist, warum welche Anzahl von Tests bei welcher Gruppe durchgeführt wird, solange also keine hohe Transparenz herrscht in Bezug auf die “Inzidenzproduktion”, ist die Bevölkerung ein Spielball derjenigen, die über diese Parameter bestimmen.